Principal components analysis
From Wikipedia, the free encyclopedia
In statistics, principal components analysis (PCA) is a technique for simplifying a data set, by reducing multidimensional data sets to lower dimensions for analysis.
Technically speaking, PCA is an orthogonal linear transformation that transforms the data to a new coordinate system such that the greatest variance by any projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so on. PCA can be used for dimensionality reduction in a data set while retaining those characteristics of the data set that contribute most to its variance, by keeping lower-order principal components and ignoring higher-order ones. Such low-order components often contain the "most important" aspects of the data. But this is not necessarily the case, depending on the application.
For a data matrix with zero empirical mean XT, (the empirical mean of the distribution has been subtracted from the data set), where each row represents a different repetition of the experiment, and each column gives the results from a particular probe, the PCA transformation is given by:
where V Σ WT is the singular value decomposition (svd) of XT.
In this article we shall adopt the other convention, so that each column is made up of results for a different subject, and each row the results from a different probe. This will mean that the PCA for our data matrix X will be given by:
where W Σ VT is the svd of X.
PCA is also called the (discrete) Karhunen-Loève transform (or KLT, named after Kari Karhunen and Michel Loève) or the Hotelling transform (in honor of Harold Hotelling). PCA has the distinction of being the optimal linear transformation for keeping the subspace that has largest variance. This advantage, however, comes at the price of greater computational requirement if compared, for example, to the discrete cosine transform. Unlike other linear transforms, PCA does not have a fixed set of basis vectors. Its basis vectors depend on the data set.
[edit] Discussion
Assuming zero empirical mean (the empirical mean of the distribution has been subtracted from the data set), the principal component w1 of a data set x can be defined as:
(See arg max for the notation.) With the first k − 1 components, the k-th component can be found by subtracting the first k − 1 principal components from x:
and by substituting this as the new data set to find a principal component in
The Karhunen-Loève transform is therefore equivalent to finding the singular value decomposition of the data matrix X,
and then obtaining the reduced-space data matrix Y by projecting X down into the reduced space defined by only the first L singular vectors, WL:
The matrix W of singular vectors of X is equivalently the matrix W of eigenvectors of the matrix of observed covariances C = X XT,
The eigenvectors with the largest eigenvalues correspond to the dimensions that have the strongest correlation in the data set (see Rayleigh quotient).
PCA is equivalent to empirical orthogonal functions (EOF).
An autoencoder neural network with a linear hidden layer is also equivalent to PCA. Upon convergence, the weight vectors of the K neurons in the hidden layer will form a basis for the space spanned by the first K principal components. Unlike PCA, this technique will not necessarily produce orthogonal vectors.
PCA is a popular technique in pattern recognition. But it is not optimized for class separability[1]. An alternative is the linear discriminant analysis, which does take this into account. PCA optimally minimizes reconstruction error under the L2 norm.
[edit] Relation to K-means clustering
It has been shown recently [2] [3] that the relaxed solution of K-means clustering, specified by the cluster indicators, are given by the PCA (principal component analysis) principal components, and the PCA subspace spanned by the principal directions is identical to the cluster centroid subspace specified by the between-class scatter matrix.
[edit] Table of symbols and abbreviations
| Symbol | Meaning | Dimensions | Indices |
|---|---|---|---|
![\mathbf{X} = \{ X[m,n] \}](http://upload.wikimedia.org/math/f/8/6/f867e7c98e184b05ed01eedf48d48da5.png) |
data matrix, consisting of the set of all data vectors, one vector per column |  |
 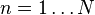 |
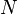 |
the number of column vectors in the data set (dimension) |  |
scalar |
 |
the number of elements in each column vector |  |
scalar |
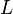 |
the number of dimensions in the dimensionally reduced subspace, 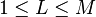 |
 |
scalar |
![\mathbf{u} = \{ u[m] \}](http://upload.wikimedia.org/math/5/c/8/5c8208a0df7d9bf4da7d597b1870f23d.png) |
vector of empirical means, one mean for each row m of the data matrix | 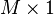 |
 |
![\mathbf{s} = \{ s[m] \}](http://upload.wikimedia.org/math/c/6/7/c676f10f15d0881db172967871693572.png) |
vector of empirical standard deviations, one standard deviation for each row m of the data matrix | 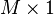 |
 |
![\mathbf{h} = \{ h[n] \}](http://upload.wikimedia.org/math/0/5/c/05c290900324b15ef4123a2293a2c544.png) |
vector of all 1's | 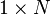 |
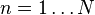 |
![\mathbf{B} = \{ B[m,n] \}](http://upload.wikimedia.org/math/3/b/0/3b00e80fb5f767ceaba11c14ffbe7ffb.png) |
deviations from the mean of each row m of the data matrix |  |
 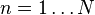 |
![\mathbf{Z} = \{ Z[m,n] \}](http://upload.wikimedia.org/math/4/e/3/4e3dbd4fb1b5ef217ba716a1a90d2511.png) |
z-scores, computed using the mean and standard deviation for each row m of the data matrix |  |
 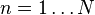 |
![\mathbf{C} = \{ C[p,q] \}](http://upload.wikimedia.org/math/a/2/a/a2ae59fecd9a30529c7ab8260e534f1a.png) |
covariance matrix |  |
  |
![\mathbf{R} = \{ R[p,q] \}](http://upload.wikimedia.org/math/0/4/2/042cc0a47cdc31cb96cd0720c0ac51b2.png) |
correlation matrix |  |
  |
![\mathbf{V} = \{ V[p,q] \}](http://upload.wikimedia.org/math/0/5/f/05f86efc393e12e96b879e1b48e9fb4f.png) |
matrix consisting of the set of all eigenvectors of C, one eigenvector per column |  |
  |
![\mathbf{D} = \{ D[p,q] \}](http://upload.wikimedia.org/math/a/c/d/acdc2b89fb7f17e8ba1abbda6f4f0a01.png) |
diagonal matrix consisting of the set of all eigenvalues of C along its principal diagonal, and 0 for all other elements |  |
  |
![\mathbf{W} = \{ W[p,q] \}](http://upload.wikimedia.org/math/0/6/1/0616329127868d5b6c7a63513a096761.png) |
matrix of basis vectors, one vector per column, where each basis vector is one of the eigenvectors of C, and where the vectors in W are a sub-set of those in V | 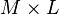 |
  |
![\mathbf{Y} = \{ Y[m,n] \}](http://upload.wikimedia.org/math/9/3/f/93ff4f2a52b9c57cb8d4d718c2ec8377.png) |
matrix consisting of N column vectors, where each vector is the projection of the corresponding data vector from matrix X onto the basis vectors contained in the columns of matrix W. |  |
 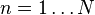 |
[edit] Algorithm #1: the covariance method
Following is a detailed description of PCA using the covariance method. The goal is to transform a given data set X of dimension M to an alternative data set Y of smaller dimension L. Equivalently, we are seeking to find the matrix Y, where Y is the Karhunen-Loeve transform (KLT) of matrix X:
[edit] Organize the data set
Suppose you have data comprising a set of observations of M variables, and you want to reduce the data so that each observation can be described with only L variables, L < M. Suppose further, that the data are arranged as a set of N data vectors  with each
with each 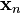 representing a single grouped observation of the M variables.
representing a single grouped observation of the M variables.
- Write
 as column vectors, each of which has M rows.
as column vectors, each of which has M rows.
- Place the column vectors into a single matrix X of dimensions M × N.
[edit] Calculate the empirical mean
- Find the empirical mean along each dimension m = 1...M.
- Place the calculated mean values into an empirical mean vector u of dimensions M × 1.
[edit] Calculate the deviations from the mean
- Subtract the empirical mean vector u from each column of the data matrix X.
- Store mean-subtracted data in the M × N matrix B.
-
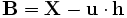
- where h is a 1 x N row vector of all 1's:
[edit] Find the covariance matrix
- Find the M × M empirical covariance matrix C from the outer product of matrix B with itself:
-
![\mathbf{C} = \mathbb{ E } \left[ \mathbf{B} \otimes \mathbf{B} \right] = \mathbb{ E } \left[ \mathbf{B} \cdot \mathbf{B}^{*} \right] = { 1 \over N } \mathbf{B} \cdot \mathbf{B}^{*}](http://upload.wikimedia.org/math/5/d/7/5d799134e511a494447178b8128021c6.png)
- where
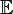 is the expected value operator,
is the expected value operator,
 is the outer product operator, and
is the outer product operator, and
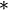 is the conjugate transpose operator.
is the conjugate transpose operator.
- where
[edit] Find the eigenvectors and eigenvalues of the covariance matrix
- Compute the matrix V of eigenvectors which diagonalizes the covariance matrix C:
- where D is the diagonal matrix of eigenvalues of C. This step will typically involve the use of a computer-based algorithm for computing eigenvectors and eigenvalues. These algorithms are readily available as sub-components of most matrix algebra systems, such as MATLAB, Mathematica or SciPy. See, for example, the eig function.
- Matrix D will take the form of an M × M diagonal matrix, where
- is the mth eigenvalue of the covariance matrix C, and
- Matrix V, also of dimension M × M, contains M column vectors, each of length M, which represent the M eigenvectors of the covariance matrix C.
- The eigenvalues and eigenvectors are ordered and paired. The mth eigenvalue corresponds to the mth eigenvector.
[edit] Rearrange the eigenvectors and eigenvalues
- Sort the columns of the eigenvector matrix V and eigenvalue matrix D in order of decreasing eigenvalue.
- Make sure to maintain the correct pairings between the columns in each matrix.
[edit] Compute the cumulative energy content for each eigenvector
- The eigenvalues represent the distribution of the source data's energy among each of the eigenvectors, where the eigenvectors form a basis for the data. The cumulative energy content g for the mth eigenvector is the sum of the energy content across all of the eigenvectors from 1 through m:
[edit] Select a subset of the eigenvectors as basis vectors
- Save the first L columns of V as the M × L matrix W:
- where
- Use the vector g as a guide in choosing an appropriate value for L. The goal is to choose as small a value of L as possible while achieving a reasonably high value of g on a percentage basis. For example, you may want to choose L so that the cumulative energy g is above a certain threshold, like 90 percent. In this case, choose the smallest value of L such that
[edit] Convert the source data to z-scores
- Create an M × 1 empirical standard deviation vector s from the square root of each element along the main diagonal of the covariance matrix C:
- Calculate the M × N z-score matrix:
-
 (divide element-by-element)
(divide element-by-element)
- Note: While this step is useful for various applications as it normalizes the data set with respect to its variance, it is not integral part of PCA/KLT!
[edit] Project the z-scores of the data onto the new basis
- The projected vectors are the columns of the matrix
- The columns of matrix Y represent the Karhunen-Loeve transforms (KLT) of the data vectors in the columns of matrix X.
[edit] Algorithm #2: the correlation method
- Editor's note: This section is currently undergoing a major revision. See page history for previous revisions.
[edit] Derivation of PCA using the covariance method
Let X be a d-dimensional random vector expressed as column vector. Without loss of generality, assume X has zero empirical mean. We want to find a  orthonormal transformation matrix P such that
orthonormal transformation matrix P such that
with the constraint that
 is a diagonal matrix and
is a diagonal matrix and 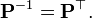
By substitution, and matrix algebra, we obtain:
We now have:
Rewrite P as d  column vectors, so
column vectors, so
and  as:
as:
Substituting into equation above, we obtain:
Notice that in  , Pi is an eigenvector of X′s covariance matrix. Therefore, by finding the eigenvectors of X′s covariance matrix, we find a projection matrix P that satisfies the original constraints.
, Pi is an eigenvector of X′s covariance matrix. Therefore, by finding the eigenvectors of X′s covariance matrix, we find a projection matrix P that satisfies the original constraints.
[edit] Correspondence analysis
Correspondence analysis is conceptually similar to PCA, but scales the data (which must be positive) so that rows and columns are treated equivalently. It is traditionally applied to contingency tables where Pearson's chi-square test has shown a relationship between rows and columns.
[edit] Software/source code
[edit] References
- Fukunaga, Keinosuke. "[2] ((1990). Introduction to Statistical Pattern Recognition. Elsevier.".
- Pearson, K. (1901). "On Lines and Planes of Closest Fit to Systems of Points in Space". Philosophical Magazine 2 (6): 559–572.
- ^ "Introduction to Statistical Pattern Recognition." [1]
- ^ H. Zha, C. Ding, M. Gu, X. He and H.D. Simon. "Spectral Relaxation for K-means Clustering", Neural Information Processing Systems vol.14 (NIPS 2001). pp. 1057-1064, Vancouver, Canada. Dec. 2001.
- ^ Chris Ding and Xiaofeng He. "K-means Clustering via Principal Component Analysis". Proc. of Int'l Conf. Machine Learning (ICML 2004), pp 225-232. July 2004.
[edit] See also
- Eigenface
- Transform coding
- Independent component analysis
- Singular value decomposition
- Factor analysis
- Kernel PCA
- PCA applied to yield curves
[edit] External links
'만들기 / Programming > research' 카테고리의 다른 글
| BRDF (0) | 2007.06.28 |
|---|---|
| Eigenvalue, eigenvector and eigenspace (0) | 2007.04.20 |
| K-nearest neighbor algorithm (1) | 2007.04.10 |
| Support vector machine (0) | 2007.04.05 |
| Image:Mandel zoom 00 mandelbrot set.jpg (0) | 2007.04.04 |



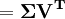
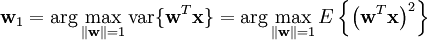






![u[m] = {1 \over N} \sum_{n=1}^N X[m,n]](http://upload.wikimedia.org/math/8/9/5/8957f38829f7b6c873a6248176f16b58.png)
![h[n] = 1 \, \qquad \qquad \mathrm{for \ } n = 1 \ldots N](http://upload.wikimedia.org/math/1/7/a/17a2338fabe95808174754e820755123.png)
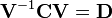
![D[p,q] = \lambda_m \qquad \mathrm{for} \qquad p = q = m](http://upload.wikimedia.org/math/e/6/4/e64dd570e3822288e9e85e0e21bda469.png)
![D[p,q] = 0 \qquad \mathrm{for} \qquad p \ne q.](http://upload.wikimedia.org/math/b/7/f/b7f35034926231465eb6593364e75729.png)
![g[m] = \sum_{q=1}^m D[p,q] \qquad \mathrm{for} \qquad p = q \qquad \mathrm{and} \qquad m = 1...M](http://upload.wikimedia.org/math/8/8/1/8815c22fd18178cd9899f2e53cb3d38b.png)
![W[p,q] = V[p,q] \qquad \mathrm{for} \qquad p = 1...M \qquad q = 1...L](http://upload.wikimedia.org/math/d/3/3/d339564d795a934c013b33047d8e9ca4.png)

![g[m=L] \ge 90%](http://upload.wikimedia.org/math/3/f/a/3fa2d24cb7d118af0e54c71037d594c0.png)
![\mathbf{s} = \{ s[m] \} = \sqrt{C[p,q]} \qquad \mathrm{for \ } p = q = m = 1 \ldots M](http://upload.wikimedia.org/math/b/7/7/b7721571befb1ed62f64d0a3fa49f426.png)
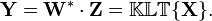

![\begin{matrix} \operatorname{cov}(\mathbf{Y}) &=& \mathbb{E}[ \mathbf{Y} \mathbf{Y}^\top]\\ \ &=& \mathbb{E}[( \mathbf{P}^\top \mathbf{X} ) ( \mathbf{P}^\top \mathbf{X} )^\top]\\ \ &=& \mathbb{E}[(\mathbf{P}^\top \mathbf{X}) (\mathbf{X}^\top \mathbf{P})] \\ \ &=& \mathbf{P}^\top \mathbb{E}[\mathbf{X} \mathbf{X}^\top] \mathbf{P} \\ \ &=& \mathbf{P}^\top \operatorname{cov}(\mathbf{X}) \mathbf{P} \end{matrix}](http://upload.wikimedia.org/math/1/9/d/19d1d26bfd1a71054cb397c331787f83.png)
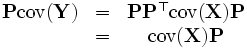
![\mathbf{P} = [P_1, P_2, \ldots, P_d]](http://upload.wikimedia.org/math/c/1/7/c1703cd93c71377fe45dab83bcb23dc4.png)

![[\lambda_1 P_1, \lambda_2 P_2, \ldots, \lambda_d P_d] = [\operatorname{cov}(X)P_1, \operatorname{cov}(X)P_2, \ldots, \operatorname{cov}(X)P_d].](http://upload.wikimedia.org/math/9/c/7/9c726ac31a4316ddded236aee1df9cbf.png)